ROC
上回我们提到,ROC 曲线就是不同的阈值下,以下两个变量的组合(如果对 Sensitivity 和 Specificity 两个术语没有概念,不妨返回,《分类模型的性能评估——以 SAS Logistic 回归为例 (1): 混淆矩阵》,强烈建议读者对着看):
Sensitivity(覆盖率,True Positive Rate)
1-Specificity (Specificity, 负例的覆盖率,True Negative Rate)
二话不说,先把它画出来(以下脚本的主体是标红部分,数据集 valid_roc,还是出自上面提到的那篇:
axis order=(0 to 1 by .1) label=none length=4in;
symbol i=join v=none c=black;
symbol2 i=join v=none c=black;
proc gplot data = valid_roc;
plot _SENSIT_*_1MSPEC_ _1MSPEC_*_1MSPEC_
/ overlay vaxis=axis haxis=axis;
run; quit;
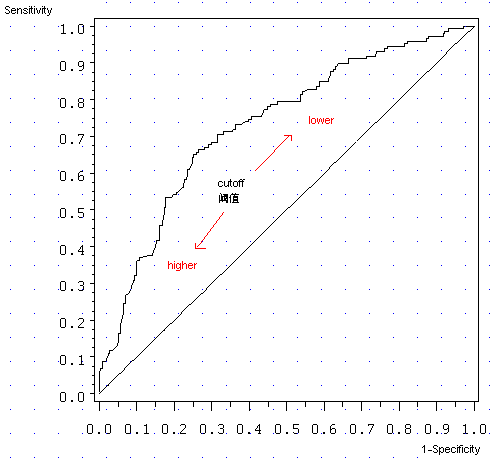
上图那条曲线就是 ROC 曲线,横轴是 1-Specificity,纵轴是 Sensitivity。以前提到过,随着阈值的减小(更多的客户就会被归为正例),Sensitivity 和 1-Specificity 也相应增加(也即 Specificity 相应减少),所以 ROC 呈递增态势(至于 ROC 曲线凹向原点而非凸向原点,不知道有无直观的解释,不提)。那条 45 度线是作为参照(baseline model)出现的,就是说,ROC 的好坏,乃是跟 45 度线相比的,怎么讲?
回到以前,我们分析 valid 数据,知道有 36.5% 的 bad 客户(Actual Positive )和 63.5% 的 good 客户 (Actual Negative)。这两个概率是根据以往的数据计算出来的,可以叫做 “先验概率”( prior probability)。后来,我们用 logistic 回归模型,再给每个客户算了一个 bad 的概率,这个概率是用模型加以修正的概率,叫做 “后验概率”(Posterior Probability)。
| 预测 | ||||
|---|---|---|---|---|
| 1 | 0 | |||
| 实 | 1 | d, True Positive | c, False Negative | c+d, Actual Positive |
| 际 | 0 | b, False Positive | a, True Negative | a+b, Actual Negative |
| b+d, Predicted Positive | a+c, Predicted Negative |
如果不用模型,我们就根据原始数据的分布来指派,随机地把客户归为某个类别,那么,你得到的 True Positive 对 False Positive 之比,应该等于 Actual Positive 对 Actual Negative 之比(你做得跟样本分布一样好)——即,,可以有,而这正好是 Sensitivity/(1-Specificity)。在不使用模型的情况下,Sensitivity 和 1-Specificity 之比恒等于 1,这就是 45 度线的来历。一个模型要有所提升,首先就应该比这个 baseline 表现要好。ROC 曲线就是来评估模型比 baseline 好坏的一个著名图例。这个可能不够直观,但可以想想线性回归的 baseline model:
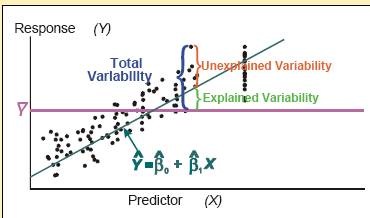
如果不用模型,对因变量的最好估计就是样本的均值(上图水平红线)。绿线是回归线(模型),回归线与水平线之间的偏离,称作 Explained Variability, 就是由模型解释了的变动,这个变动(在方差分析里,又称作 model sum of squares, SSM)越大,模型表现就越好了(决定系数 R-square 标准)。同样的类比,ROC 曲线与 45 度线偏离越大,模型的效果就越好。最好好到什么程度呢?
在最好的情况下,Sensitivity 为 1(正确预测到的正例就刚好等于实际的正例总数),同时 Specificity 为 1(正确预测到的负例个数就刚好等于实际的负例数),在上图中,就是左上方的点 (0,1)。因此,ROC 曲线越往左上方靠拢,Sensitivity 和 Specificity 就越大,模型的预测效果就越好。同样的思路,你还可以解释为什么 ROC 曲线经过点(0,0) 和(1.1),不提。
AUC, Area Under the ROC Curve
ROC 曲线是根据与 45 度线的偏离来判断模型好坏。图示的好处是直观,不足就是不够精确。到底好在哪里,好了多少?这就要涉及另一个术语,AUC(Area Under the ROC Curve,ROC 曲线下的面积),不过也不是新东西,只是 ROC 的一个派生而已。
回到先前那张 ROC 曲线图。45 度线下的面积是 0.5,ROC 曲线与它偏离越大,ROC 曲线就越向左上方靠拢,它下面的面积 (AUC) 也就应该越大。我们就可以根据 AUC 的值与 0.5 相比,来评估一个分类模型的预测效果。
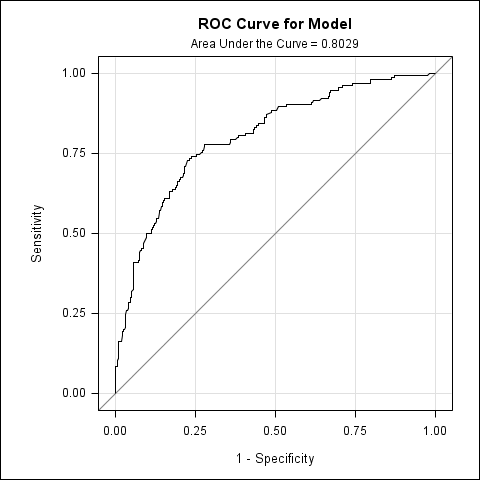
SAS 的 Logistic 回归能够后直接生成 AUC 值。跑完上面的模型,你可以在结果报告的 Association Statistics 找到一个叫 c 的指标,它就是 AUC(本例中,c=AUC=0.803,45 度线的 c=0.5)。
注:以上提到的 c 不是 AUC 里面那个’C’。这个 c 是一个叫 Wilcoxon-Mann-Whitney 检验的统计量。这个说来话长,不过这个 c 却等价于 ROC 曲线下的面积(AUC)。
ROC、AUC:SAS9.2 一步到位
SAS9.2 有个非常好的新功能,叫 ODS Statistical Graphics,有兴趣可以去它主页看看。在 SAS9.2 平台提交以下代码,Logistic 回归参数估计和 ROC 曲线、AUC 值等结果就能一起出来(有了上面的铺垫,就不惧这个黑箱了):
ods graphics on;
proc logistic data=train plots(only)=roc;
model good_bad=checking history duration savings property;
run;
ods graphics off;
这个 ROC 图貌似还漂亮些,眼神好能看见标出来的 AUC 是 0.8029。 最后提一句,ROC 全称是 Receiver Operating Characteristic Curve,中文叫 “接受者操作特性曲线”,江湖黑话了(有朋友能不能出来解释一下,谁是 Receiver,为什么 Operating,何谓 Characteristic——这个看着好像是 Sensitivity 和 Specificity),不过并不妨碍我们使用 ROC 作为模型评估的工具。
下期预告:Lift 和 Gain
不多说,只提一句,跟 ROC 类似,Lift(提升)和 Gain(增益)也一样能简单地从以前的 Confusion Matrix 以及 Sensitivity、Specificity 等信息中推导而来,也有跟一个 baseline model 的比较,然后也是很容易画出来,很容易解释。
参考资料
- Mithat Gonen. 2007. Analyzing Receiver Operating Characteristic Curves with SAS. Cary, NC: SAS Institute Inc.
- Mike Patetta. 2008. Categorical Data Analysis Using Logistic Regression Course Notes. Cary, NC: SAS Institute Inc.
- Dan Kelly, etc. 2007. Predictive Modeling Using Logistic Regression Course Notes. Cary, NC: SAS Institute Inc.
- Receiver operating characteristic, see http://en.wikipedia.org/wiki/Receiver_operating_characteristic
- The magnificent ROC, see http://www.anaesthetist.com/mnm/stats/roc/Findex.htm

发表 / 查看评论