为什么统计学家也应该学学 TensorFlow

（先啰嗦一句：本文的标题和内容牵涉到 TensorFlow，只是因为它是可用的工具之一，我相信很多其他的框架都可以做到文中我想要实现的功能。我自己并没有工具上的偏好，所以就当是拿 TensorFlow 举一个例子。）

对于学统计做统计的人来说，这可能是最好的时代，也可能是最坏的时代。好的地方我就不多说了，基本上关键词包括“大数据”、“数据科学”等，搜索引擎可以帮你列举出许多激动人心的字眼。为什么会坏呢？因为统计的很多传统优势正在逐渐被各种机器学习算法取代，因此许多统计的核心元素，要么因为适应不了新形式的数据而被边缘化，要么因为在机器学习中有广泛应用而被有意无意地同化到了机器学习当中。

面对机器学习，或者进一步缩小范围，面对当前火热的深度学习，我陆陆续续找了一些做统计的老师和朋友聊过这个话题，发现有两类观点比较明显。第一类是深度学习“威胁论”，主要的意思是统计学被蚕食得非常严重，很多原来统计的阵地，不管是方法论上的还是现实案例中的，都被深度学习取代了。另一类是“否定论”，认为深度学习大部分是在炒作，在一些特定的行业（例如制药），传统统计依然处于核心地位，因此无需过于担心。

每次聊完之后我都会觉得“哇，对啊对啊，好有道理”，但转念一想总觉得哪里不对劲——为什么没有一种“学习论”呢？我觉得在很多情况下，人们对于新生的事物都有一种天然的抵触感，然而如今面对深度学习的火热趋势，你可以拥护它，也可以批判它，但惟一做不到的就是去忽视它。相反，当你试着去了解和学习这些新的事物，你会发现它给你带来的好处可能要远远多于坏处。

当然，这篇文章并不想过多讨论这类高层次的问题。之所以写这一篇，是想以一些自己的经历和体验来说明为什么我们应该去尝试了解和学习一些新生的事物。

暑假的时候，利用一些空余的时间看了看 TensorFlow 的文档。在我以前的印象中，TensorFlow 是为深度学习而设计的，如果我的研究或工作不涉及深度学习，我就应该永远也用不到它。就是因为有这种刻板印象，一直以来我对于这类软件和工具都处于一种旁观的态度。

然而当你实际迈出了第一步时，你就会发现很多事情并不是之前想像的那样。比如对于 TensorFlow，你会发现其核心组件跟深度学习没有半毛钱关系。如果使用得当，你完全可以把 TensorFlow 打造成一个强大的帮助你进行统计建模和求解的工具。这是我在统计这个大湖里泡了蛮久，然后又在新的水源中找到一片活水时所收获的惊喜。

上个学期参加了一个讨论班，组织的老师吐槽说，我们学统计的，重心大都在模型的估计和推断上，却忽视了建模的过程。其后果就是，为了估计和推断能有比较简单的形式，往往会在建模上进行简化，这就造成了很多统计模型在实际中并不实用。如果有一种办法，能让统计学家更专注于模型的搭建，而让计算机去完成大部分的求解工作，那么统计应该就会有更广阔的应用空间。

于是在我接触了 TensorFlow 之后，我发现它正好对上面的这个疑问提供了一个回应。TensorFlow 的核心部件，大部分是一些针对向量和矩阵（或者更一般地说是张量，也就是 TensorFlow 名称中的 Tensor）的运算符。这些运算符本质上是从输入变量到输出变量的一个映射，比如计算均值的运算符，输入一个向量，就可以得到一个标量的输出，又或者矩阵乘法运算符，输入两个矩阵，可以输出一个新矩阵。更重要的是，这些运算符包含了输入输出间导数（或者梯度）的信息，因此给定输入的数值，程序可以计算出输出对于输入的梯度，反之亦然。这样一来的结果就是，借助自动微分的技术，当你定义了一连串的运算后，计算机就可以自动帮你计算整个输入输出间的梯度。而我们知道，许多统计模型最后都依赖于极大似然估计，而对极大似然的最优化，最经典的办法就是梯度下降法，因此当梯度计算出来了，模型的求解就完成了一大半。

当统计学家从繁复的导数计算中解放出来了，他们就可以用更多的时间来愉快地加班建模了。

说了这么多，该用一个实际的例子来展示一下被释放的小宇宙生产力了。我们来考虑一个简单但非常实用的统计模型：混合分布的参数估计。下面这段 Python 代码生成了一组服从 $0.3\cdot N(0,1)+0.7\cdot N(5,1.5^2)$ 混合分布的模拟数据。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(123)

# Parameters
p1 = 0.3
p2 = 0.7
mu1 = 0.0
mu2 = 5.0
sigma1 = 1.0
sigma2 = 1.5

# Simulate data
N = 1000
x = np.zeros(N)
ind = np.random.binomial(1, p1, N).astype('bool_')
n1 = ind.sum()
x[ind] = np.random.normal(mu1, sigma1, n1)
x[np.logical_not(ind)] = np.random.normal(mu2, sigma2, N - n1)

# Histogram
plt.hist(x, bins=30)
plt.show()

假设我们用的是“真实”的模型，也就是 $p_1 N(\mu_1,\sigma_1^2)+p_2 N(\mu_2,\sigma_2^2)$，那么接下来的任务就是用极大似然的方法来估计这些未知参数的取值。

看到这里，你可能已经意识到，这是一个高斯混合模型（GMM），通常的解法是 EM 算法。但在这里作为展示，我们依然采用梯度的办法，而且另外一个好处是可以方便地扩展到其他的分布。利用 TensorFlow，我们可以用如下的代码来进行模型估计：

import tensorflow as tf
import tensorflow.contrib.distributions as ds

# Define data
t_x = tf.placeholder(tf.float32)

# Define parameters
t_p1_ = tf.Variable(0.0, dtype=tf.float32)
t_p1 = tf.nn.softplus(t_p1_)
t_mu1 = tf.Variable(0.0, dtype=tf.float32)
t_mu2 = tf.Variable(1.0, dtype=tf.float32)
t_sigma1_ = tf.Variable(1.0, dtype=tf.float32)
t_sigma1 = tf.nn.softplus(t_sigma1_)
t_sigma2_ = tf.Variable(1.0, dtype=tf.float32)
t_sigma2 = tf.nn.softplus(t_sigma2_)

# Define model and objective function
t_gm = ds.Mixture(
    cat=ds.Categorical(probs=[t_p1, 1.0 - t_p1]),
    components=[
        ds.Normal(t_mu1, t_sigma1),
        ds.Normal(t_mu2, t_sigma2)
    ]
)
t_ll = tf.reduce_mean(t_gm.log_prob(t_x))

# Optimization
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(-t_ll)

# Run
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
for _ in range(500):
    sess.run(train, {t_x: x})

print('Estimated values:', sess.run([t_p1, t_mu1, t_mu2, t_sigma1, t_sigma2]))
print('True values:', [p1, mu1, mu2, sigma1, sigma2])

其输出结果为

Estimated values: [0.29020751, -0.078560337, 5.0137568, 0.95754921, 1.4157518]
True values: [0.3, 0.0, 5.0, 1.0, 1.5]

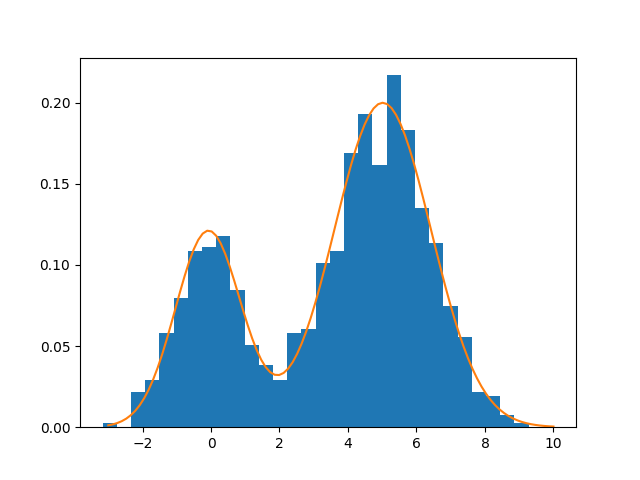
可以看出来，估计的结果和真值是非常接近的。下图中的黄线展示了估计出来的密度曲线。

这段 TensorFlow 程序其实非常贴合统计建模的思路：首先我们收集到了一组数据，然后我们对它的分布进行了假设，该分布依赖于若干未知的参数，而估计参数的方法是极大似然法，即参数的估计值应该最大化这组数据的似然函数值。回到之前的程序，可以看出其整个流程也基本符合这一思路。在这里我稍微对其中用到的函数做一些解释，更详细的介绍可以去查阅 TensorFlow 的官方文档。

首先，我们定义一个结构 t_x 用来表示观测到的数据，这里 placeholder 的意思是我们先给这个变量“占一个位”，其实际的数值会在之后予以提供。后面有一连串的 Variable，是 TensorFlow 中用来表达待估参数的一种方式，括号中的第一个数是我们提供的初值。其中我们还用到了一个 softplus 运算符，这是为了照顾那些恒正的参数而做的一个变换，等价于函数 log(exp(x) + 1)。在这之后就是定义我们的混合分布模型，可以看到该模型的参数都依赖于之前定义的 Variable 对象，而我们的目标函数就是该混合分布在数据上的对数似然函数值，我们把它存储在 t_ll 变量中。

定义好这个模型后，TensorFlow 就可以自动计算 t_ll 相对于 t_p1_，t_mu1 等参数的导数，而利用 TensorFlow 提供的最优化工具，我们只需要反复迭代更新参数，直到满足收敛条件就可以了。

整个过程中，我们几乎只需要把我们脑海中的模型用 TensorFlow 内置的运算符表达出来，其余的工作都可以自动化或半自动化地完成。由于导数也是由自动微分完成的，所以我们甚至连公式的推导都可以进一步简化。此外，如果你想把混合分布的成分改成 t-分布，或是想把其中的某个参数改成其他协变量的线性函数，你只需要改变一下参数和模型的定义，几乎没有多少额外的工作，这可以说是对统计建模一次巨大的改革。

说了这么多，无非就是想告诉大家，他山之石，可以攻玉。在面对层出不穷的新技术时，当时我也是拒绝的，但只有亲身尝试了之后，才能够切实对这些技术做出一些更为客观的评价。写这篇文章，也是希望能给身在统计圈的各位提供一些启发。数据科学也好，深度学习也好，事实是这些新名词已经诞生了，并且还附带了一系列的并发效应。除了吹与黑，每个人都有的第三种选择就是去主动拥抱这些新的知识和技术，然后去思考如何利用他们来为自己的研究和工作提供便利。